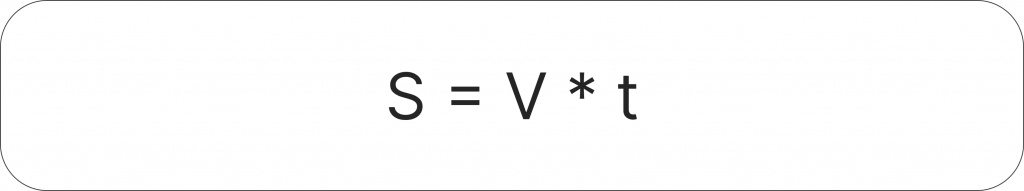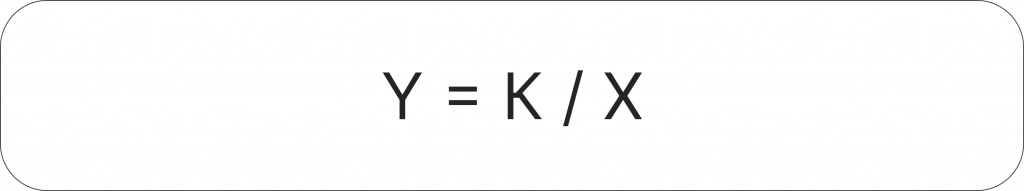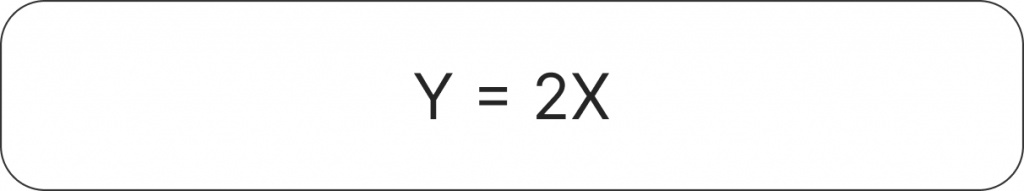Аргумент функции: что это

Аргумент и функции

В нашей жизни происходят определенные процессы, где можно наблюдать, как величины меняются в зависимости друг от друга.

Так, например, одно и то же расстояние на автомобиле преодолевают быстрее, чем пешком. Стоимость покупки зависит от количества предметов в чеке — чем больше купил, тем больше потратил. Количество годичных колец зависит от возраста дерева — чем оно старше, тем колец больше. 

В этих примерах одни значения напрямую зависят от других. Только одни из них независимы — скорость, количество товаров и колец. А вторые меняются — расстояние, стоимость чека, возраст дерева.

Аргумент — это независимая переменная, над которой совершается алгебраическое действие и определяется значение функции. В уравнениях с одной неизвестной, как правило, обозначается литерой X.

Все перечисленные процессы, если перевести их на язык математики, называются взаимосвязью аргумента и функции.

Функция — это значение, которое определяют с помощью переменной. То есть величина функции зависит от аргумента. В общем виде функция записывается как Y = F(X).

Простой пример аргумента и функции в реальной жизни:

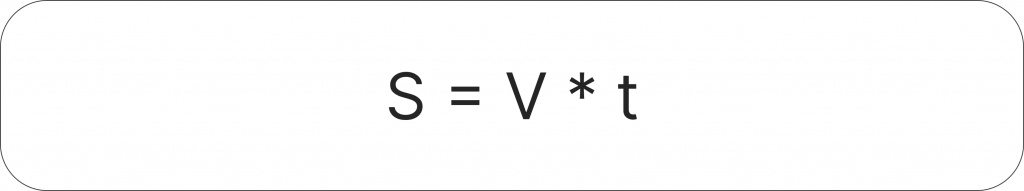
где:

• S — расстояние (функция)

• V — скорость (аргумент)

•  t — время

На автомобиле со скоростью 40 км/ч за 30 минут преодолеют 20 км (40 км/ч * 0,5 часа). Пешком со скоростью 6 км/ч за то же время расстояние составит всего 3 км.

Вывод: чем выше скорость (аргумент), тем больше расстояние (функция).

Прямая и обратная зависимость

Аргумент и функция взаимозависимы. Другими словами, когда изменяется X, соответственно, меняется Y.

Функциональная зависимость может быть прямо и обратно пропорциональной. Рассмотрим каждую подробнее.

Прямая пропорция

Прямая пропорция — это свойство двух переменных, при котором изменение одной величины вызывает пропорциональное изменение другой.

Например, закон теплового расширения:

где:

• Vo — начальный объем газа (аргумент)

• t — разность начальной и конечной температур

• α — коэффициент теплового расширения газов одинаковый для всех газов

Из данного закона следует, что чем выше температура, тем больше объем газа. То есть усматривается прямая зависимость между объемом и температурой. В алгебре это называют прямая пропорциональность.

Пример задачи на прямую пропорцию:

За 10 дней журналист сдает в печать 20 статей. Сколько журналистов должно работать, чтобы написать 60 статей за 10 дней, если они пишут с такой же скоростью?

Решение:

20 (статей) / 10 (дней) * Х (помощников) = 60 (статей) / 10 (дней)

20/10*Х = 60 / 10 Х = (60/10) / (20/10)

Х = 3

Ответ: три человека напишут за 10 дней 60 статей.

Вывод: чем больше людей, тем больше объем выполненной работы.

Обратная пропорция

Обратная пропорция — это зависимость, при которой уменьшение одного числа ведет к кратному увеличению другого и наоборот.

Для удобства обратную пропорцию можно представить в виде формулы:

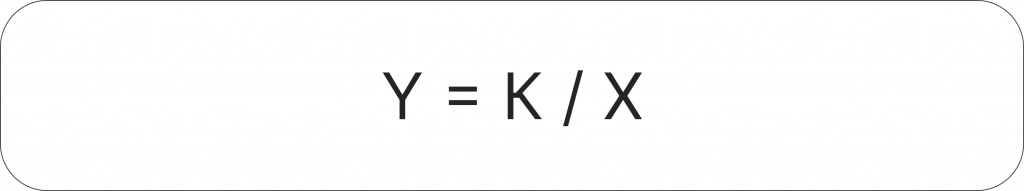
где:

• Y — зависимое число (функция)

• X — независимая переменная (аргумент)

• К — постоянная величина, которую именуют коэффициентом обратной пропорциональности

Пример обратной пропорции:

Кролик съедает пять морковок в день. 30 морковок ему хватит на шесть дней. Если кроликов будет двое, морковок хватит на три дня. Если кроликов будет трое — всего на один день.

Вывод: чем больше кроликов, тем быстрее закончится корм.

Основные характеристики функции

В алгебре и начале анализа зависимость переменной Y от переменной X имеет ряд характеристик:

Область определения и область значений

Область определения функции — все допустимые значения аргумента X, при которых функция Y = F(X) определена, то есть имеет смысл.

Формула функции должна соответствовать двум законам:

• Нельзя делить на ноль — знаменатели дробей с X не должны быть равны 0

• Извлечение корня из отрицательного числа невозможно, поскольку любое число, даже отрицательное, при возведении в квадрат будет положительным

Область значений функции — это множество всех действительных значений Y, которые принимает функция.

Функцию задают с помощью формул, таблиц, графиков, словесных описаний

Пример формулы:

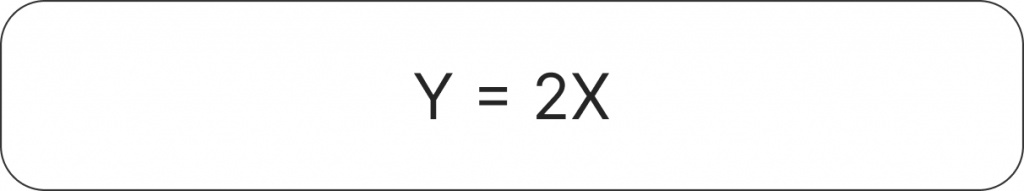
Любое действительное число Y всегда будет в два раза больше, чем X.

Пример табличного задания функции:

Необходимо построить график из данных в таблице:

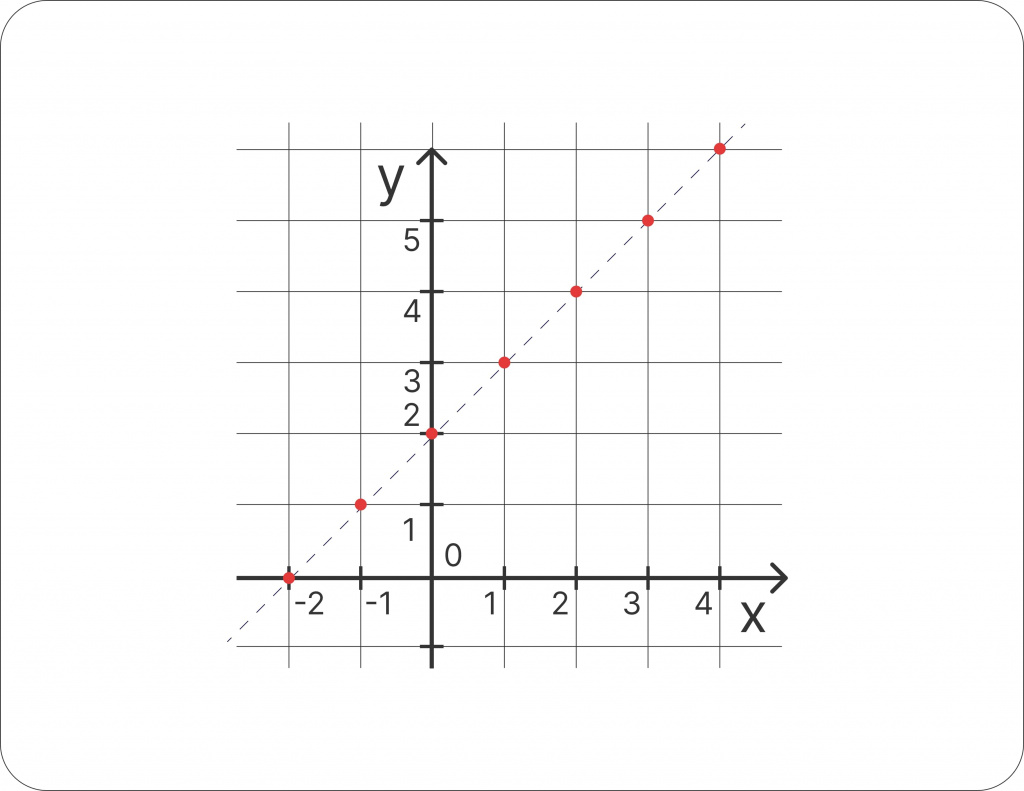
Табличный способ считается более удобным, так как все значения уже занесены в таблицу. При построении графика не надо проводить вычислений.

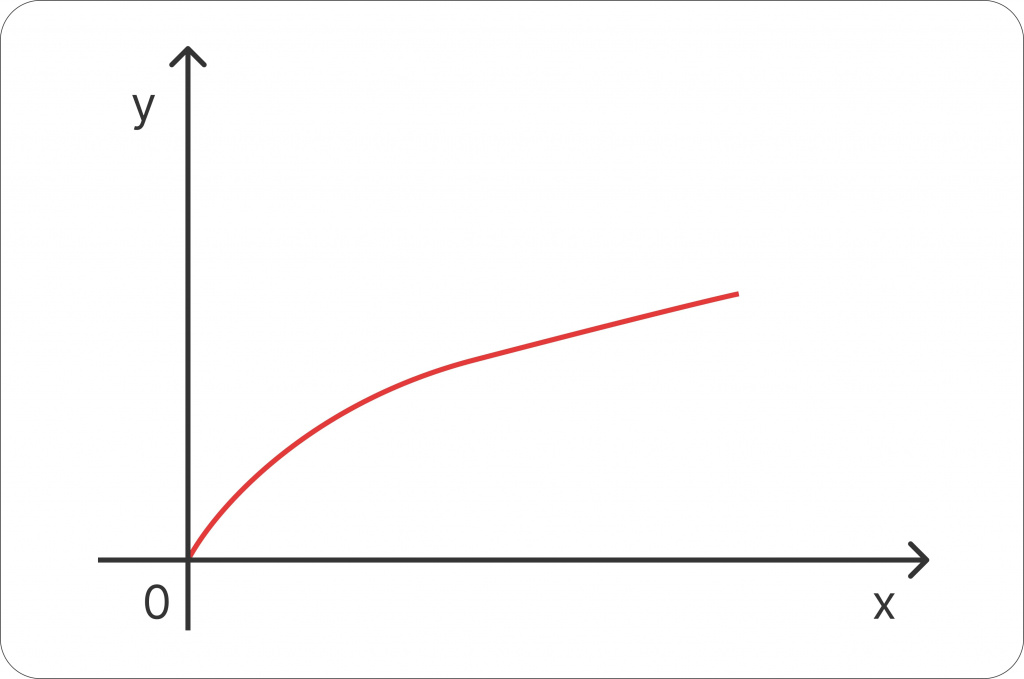
Пример построения графика по формуле:

Поиск значений Y = √X

Поскольку квадратного корня из отрицательных чисел не существует, значение X всегда будет ⩾0

Пример словесного описания:

Каждому целому числу соответствует его квадрат Y = X2

Областью определения будет множество целых чисел, областью значений — множество квадратов натуральных чисел, включая 0.

Нули функции

Заданное значение аргумента, при котором значение функции будет равно нулю.

В алгебре подобные задачи решают с помощью уравнения с одним неизвестным. Для определения значения достаточно вместо Y подставить ноль и решать:

14X + 16 = 0

14X = –16

X = –16/14

X = –8/7

Вместо заключения

Аргумент и функция — основы функциональной алгебры, понимание которых дает возможность разобраться в предмете. Мы постарались простыми словами и на понятных примерах объяснить, что такое аргумент и как определить функцию, которая зависит от значения аргумента.