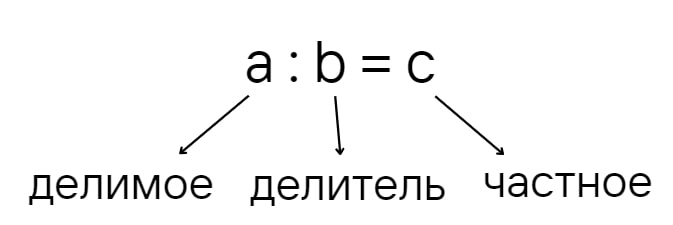Что такое частное число

Деление как основная математическая операция

В математике есть четыре базовые операции: сложение, вычитание, умножение и деление. Частное чисел — понятие, связанное с делением, поэтому имеет смысл рассмотреть эту операцию подробнее.

Деление — математическое действие, обратное умножению. Оно позволяет найти один из сомножителей по произведению и второму множителю.

При письме число обозначается:

1. Двоеточием. Впервые применяется Готфридом Лейбницем в статье, размещенной в журнале «Acta Eruditorum» в 1684 году
2. Обелюсом или английским знаком деления. Символ впервые использован швейцарским математиком Иоганном Раном в книге «Teutsche Algebra», датируемой 1659 годом
3. Косой чертой. Предположительно, самый старый символ, который использовался английским математиком Уильямом Отредом в работе «Clavis Mathematicae», опубликованной в 1631 году
4. В виде дроби

В отечественной традиции чаще всего используется двоеточие, в компьютерных нотациях — косая линия.

Делимое, делитель и частное: чем они отличаются

Стандартный пример на деление записывается так: a : b = c, где:

1. a — это делимое
2. b — делитель
3. c — частное 

По сути, деление — это гипероператор вычитания.

Частное — это результат деления одного числа на другое, оно показывает, во сколько раз число «a» больше, чем «b».

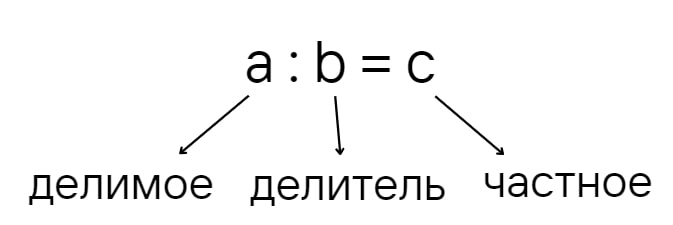
В случае с делением результат изменяется от перестановки элементов операции. Процесс не ассоциативен: при последовательном делении трех чисел итоговое число зависит от порядка выполнения операций. Это свойство иллюстрирует формула: (a:b):c≠a:(b:c).

Деление — операция, обратная умножению, что можно использовать для проверки результата. Умножьте частное «c» на делитель «b». Если расчеты верны, в результате вы должны получить делимое «a».

Полное и неполное частное

Рассмотрим простейший пример деления: 80 : 40 = 2. Мы видим, что делимое тут больше делителя в 2 раза, а деление происходит без остатка. Частное в таком случае называется полным.

Возможны ситуации, когда при делении возникает остаток. Возьмем пример: 75 : 6. В этом случае получить целое число не получится, так как 75 не делится на 6 без остатка. Целое число 6 содержится в 75 двенадцать раз. Умножив 6 на 12, мы получим 72, а отняв результат от 75 — 3. Следовательно, тут:

• 75 — делимое

• 6 — делитель

• 12 — неполное частное

• 3 — остаток

Неполное частное — это результат деления с остатком. Вкратце описать этот процесс можно формулой: a = b * c + r, где a — делимое, b — делитель, c — неполное частное, а r — остаток.

Подобная операция называется целочисленным делением, а поиск r — взятием остатка. Подобные вычисления используются в программировании, криптографии, арифметике, алгебре, при изучении теории чисел.

Пример целочисленного деления

У повара есть 35 яблок, из которых он хочет приготовить компот. Известно, что на один литр уходит три яблока. Сколько целых литров компота сможет приготовить повар и сколько яблок у него останется?

Условия этой задачи предполагают взятие остатка. Необходимо провести целочисленное деление, разделив 35 на 3. Частным в данном случае будет число 11, а остатком — 2.

Проверим результат умножением: 35 = 11 * 3 + 2.

Согласно правилам арифметики, умножение выполняется первым. Мы получаем 33, а при добавлении 2 — 35.

Следующее натуральное число 12 не подходит, поскольку при умножении 12 на 3 мы получаем 36, что на один больше, чем делимое.

Следовательно, повар сможет приготовить 11 литров компота, и у него останется два яблока. На 12 литров ему не хватает еще одного яблока.

Если бы в задаче не требовалось вычислить остаток, частное бы стало дробным числом. В этом случае после целого числа 11 ставится запятая, после которой вписывается результат деления остатка на делитель (35 на 3). Тогда бы частное выглядело как 11,66666666666667.

Результат допустимо округлить и записать в ответ, что из 35 яблок повар смог бы приготовить 11 литров и 667 миллилитров компота.

Как удобнее всего вычислить частное

Деление — операция, обратная умножению. Поэтому в ряде случаев можно использовать таблицу умножения. Это называется табличным делением: оно возможно, если делимое является табличным значением, а делитель — однозначным числом. Так, если 3 * 5 = 15, то 15 : 3 = 5, а 15 : 5 = 3.

Если табличное деление не применимо, можно использовать деление в столбик, схема которого представлена на рисунке ниже.

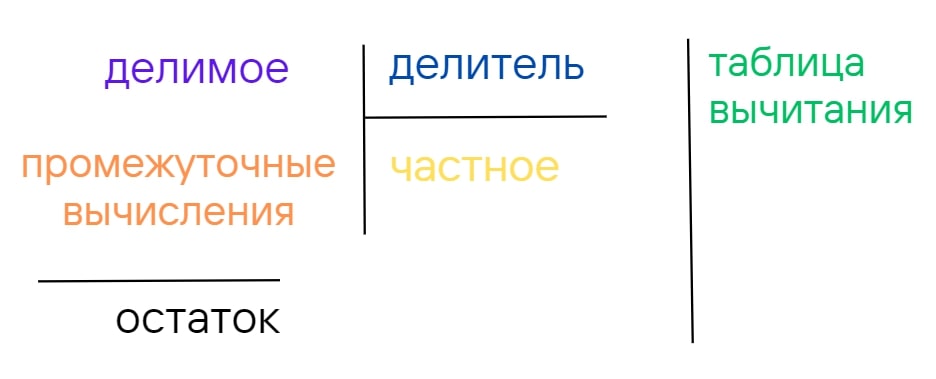
Разберем, как это работает, на примере уже упомянутой задачи с яблоками. Запишем данные таким образом: 35|3. Возьмем первую цифру делимого. Она равна делителю, а значит, при делении мы получим единицу. Пишем ее в частное.

Берем вторую цифру делимого — 5. Мы знаем, что результат умножения 3 * 2 = 6, поэтому единственное доступное целое число тут — единица: 3 * 1 = 3.

Пишем единицу в частное, а в промежуточных вычислениях отнимаем тройку от пятерки, получая на выходе 2.

Два меньше трех, поэтому в зависимости от условий задачи, либо пишем ее в остаток, оставляя в частном 11, либо добавляем к двойке ноль, получая двадцать. При делении 20 на 3 мы получаем 6 (3 * 6 = 18) и 2 в остатке (20 - 18 = 2). Шестерка пишется в частное после запятой. Процесс можно продолжать бесконечно, поэтому допустимо округлить результат, получив уже упомянутое число 11,66666666666667.

Есть еще несколько хитростей, облегчающих деление. Так, при работе с круглыми числами, оканчивающимися на ноль, их можно не учитывать в расчетах.

В примере 30 : 3 можно временно отбросить ноль, после чего тот приобретет вид 3 : 3. Просто пишем в частное единицу и подставляем то количество нулей, которое мы убрали из делимого.

Если мы делим два круглых числа, допустимо отбросить одинаковое количество нулей в делимом и делителе: 300 : 30 = 30 : 3 = 10.

Еще один вариант — использовать разрядные слагаемые. Записываем многозначное число как сумму круглых и однозначных. Так, 48 будет выглядеть как 40+8, а деление 48 : 4 как 40 : 4 + 8 : 4 = 10 + 2 = 12.

Если способ не помогает, можно методом подбора поискать удобные слагаемые. Желательно, чтобы первым тут выступало максимально большое круглое число, которое без остатка делится на делитель. Так, пример 75 : 5 можно представить в виде 50 : 5 + 25 : 5 = 10 + 5 = 15.

Вывод: частное чисел — одно из базовых понятий в арифметике, связанное с операцией деления. Получить его можно, разделив делимое на делитель. Частное показывает, во сколько раз первое число больше второго.