Что такое медиана треугольника

Медиана: что это и как ее найти

Медианой в геометрии называют луч, соединяющий вершину (угол) с противоположной гранью строго посредине.

Начертить ее можно двумя простыми действиями:

1. Разбиваем одну из граней фигуры на две равные части и маркируем точкой
2. Проводим линию, которая соединит указанную точку с противолежащим углом

На рисунке ниже показан произвольный треугольник АВС, у которого из вершины А к стороне ВС проведена линия. Точка пересечения М является серединой стороны ВС, а отрезок АМ — это и будет медиана.

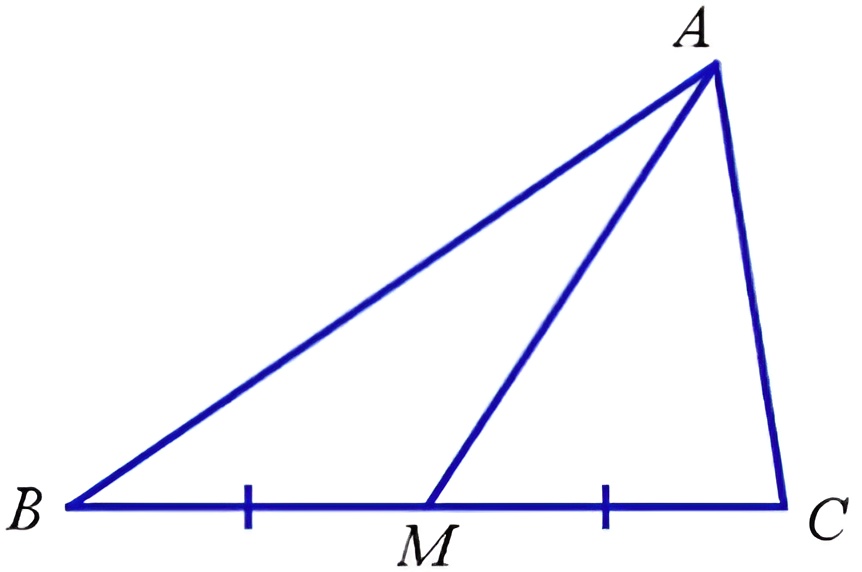
Медиана делит фигуру на два равновеликих треугольника, каждый из которых обладает одинаковой площадью.

Понятия медианы, высоты и биссектрисы

Всего существует три типа линий, соединяющих углы с противолежащими гранями. Рассмотрим их подробнее.

Медиана

Количество сторон и углов в любом треугольнике будет всегда равняться трем. В одной фигуре можно начертить только три медианы, при этом все они пересекутся в единой точке. Наглядно это можно увидеть на рисунке ниже:

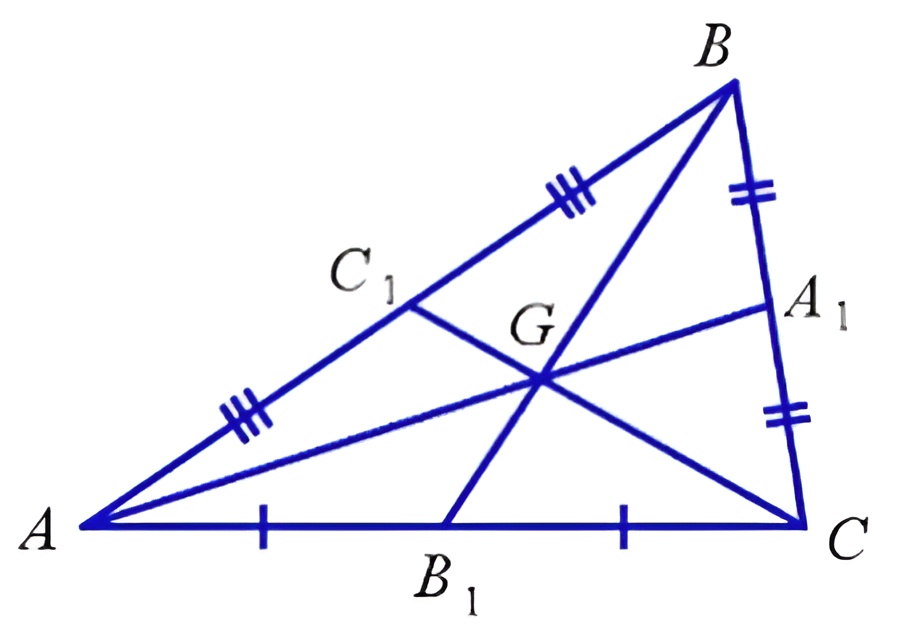
В нашем случае у фигуры АВС проведены три луча: АА1, ВВ1 и СС1, а точка, где они сходятся, — это G.

Биссектриса

Биссектрисой называют луч, исходящий из любого угла к противоположной стороне. В отличие от медианы, он делит угол на две равные половины, а не сторону, поэтому точки пересечения обеих линий с общей гранью могут быть разными.

Начертить биссектрису не сложно, достаточно выполнить три простые действия:

1. Провести луч из любой точки (А, В, С) фигуры так, чтобы он разделил угол пополам
2. Зафиксировать точку на противолежащей стороне фигуры
3. Соединить общей линией отрезок между точками входа и выхода

В качестве примера рассмотрим рисунок ниже:

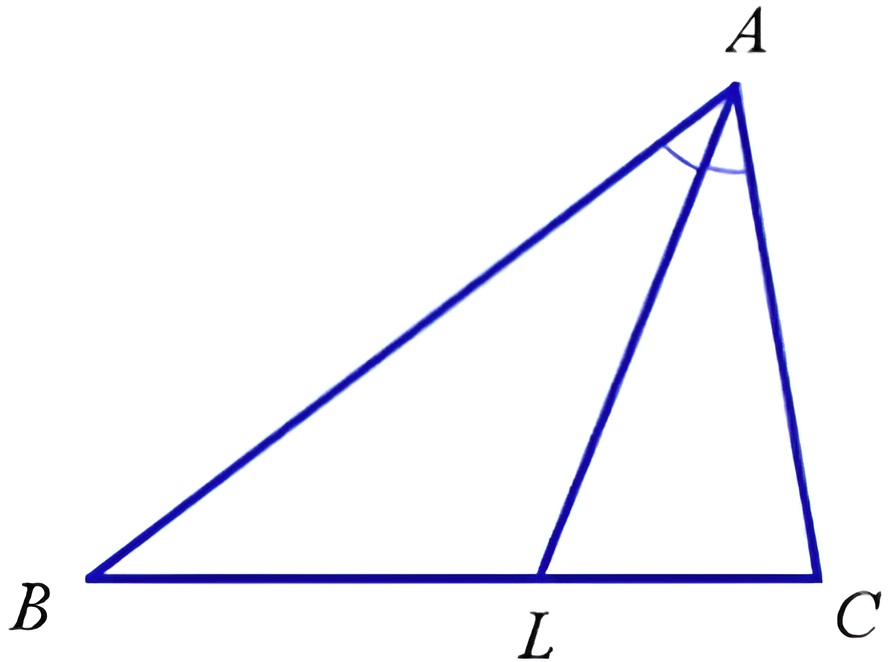
В нашем случае у треугольника АВС из вершины А проходит линия, разделяющая угол пополам. Место пересечения с гранью фигуры обозначено буквой L, соответственно, линия AL будет биссектрисой.

Высота

Еще одна линия, которая может соединять угол и противолежащую грань фигуры, — это высота. Она всегда будет перпендикулярна к отрезку, с которым пересекается.

Правильно определить высоту у фигур разного типа поможет наглядный рисунок ниже:

Вне зависимости от того, из какого угла проведена высота, она всегда будет перпендикуляром, но не всегда будет находиться внутри фигуры. 

В качестве примера рассмотрим средний треугольник АВС, в котором из вершины В (острый угол) опускается прямая линия на сторону АС. Из-за того, что вершина А образует тупой угол, перпендикуляр не может ее пересечь внутри поля фигуры. Чтобы найти точку пересечения, необходимо продлить линию АС влево. В этом случае высотой будет линия ВD.

Если из одного угла произвольного треугольника провести все три линии, то длина медианы окажется наибольшей, а высота будет самой короткой.

Равнобедренный треугольник и медиана

Равнобедренным треугольником называют фигуру, у которой есть две одинаковые по размеру стороны. Такие грани называются боковыми, а нижняя — это основание. Как выглядит такая фигура, можно увидеть на рисунке ниже:

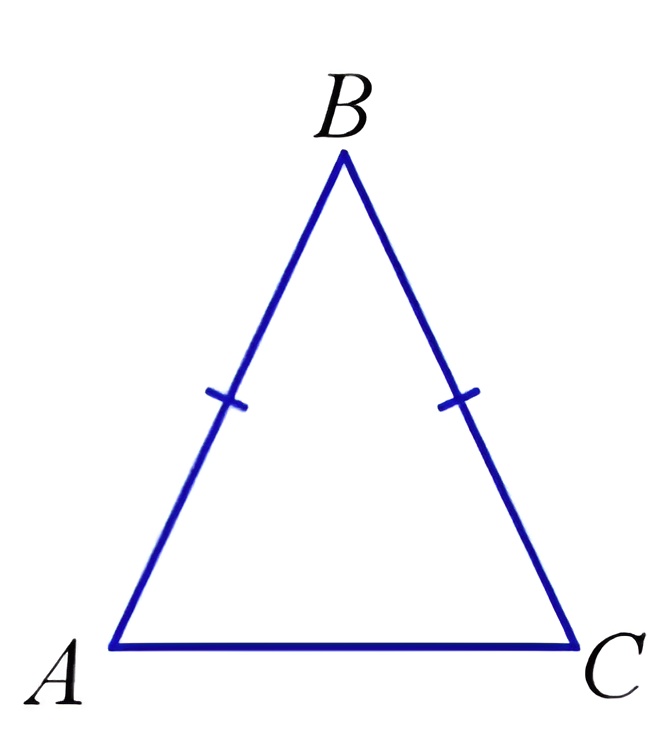
Особенность такой фигуры — равные углы при точках А и С. При проведении луча из верхнего угла В к основанию медианы получаем линию, которая по расположению и размеру будет совпадать с высотой и биссектрисой. Как это выглядит, наглядно представлено на рисунке ниже:

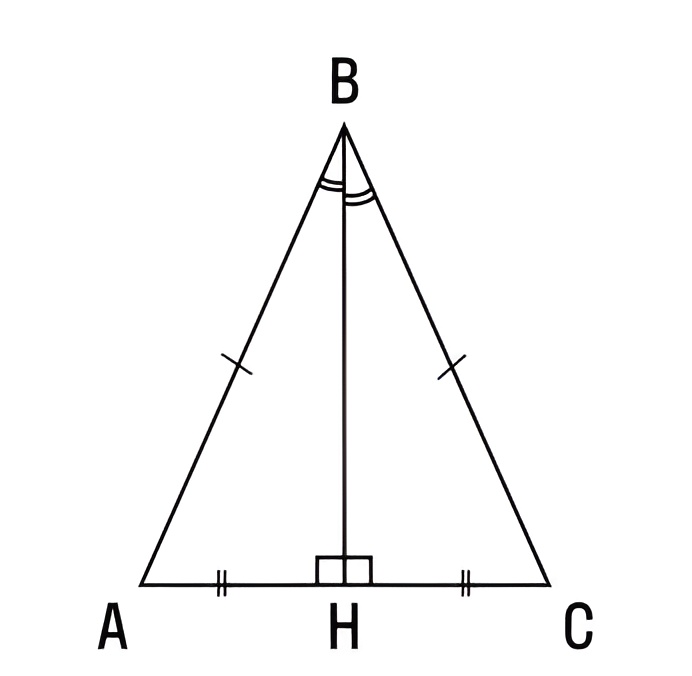
Как это доказать, рассмотрим на простом примере. Первое, что нам понадобится, — это доказательство того, что фигуры АВН и СВН симметричны.

Для этого представим, что ВН будет биссектрисой. Учитывая, что речь идет о равнобедренном треугольнике, грани АВ и ВС равны по своей длине.

Угол А равен углу С, как и оба угла при общей вершине В (свойство биссектрисы). При этом ВН — это общая грань, значит, треугольники АВН и СВН одинаковы.

Отрезки АН и СН также равны, поэтому ВН — это медиана. При одинаковых значениях углов у точек А и С сумма двух углов по обе стороны от точки Н будет равна 180 градусов. Значит, каждый угол равен 90 градусов, что доказывает, что ВН — это высота.

Итог: любой луч, который можно провести из верхней точки треугольника перпендикулярно основанию, будет совмещать в себе высоту, медиану и биссектрису.

Задача

Дано: треугольник АВС разделен на два треугольника АВМ и АСМ медианой АМ. Площадь АВС равна 80 см, площадь АВМ равна 48 см, площадь АСМ равна 66 см.

Решение:

Медиана АМ является общей стороной для малых фигур и входит в периметр основного треугольника АВС. Для составления математического уравнения обозначим медиану как Х. Теперь запишем периметры обоих малых фигур как сумму всех сторон:

Для треугольника АВМ формула периметра выглядит так: АВ + ВМ + Х = 48 см

Для треугольника АСМ получаем аналогичную формулу: АС + СМ + Х = 66 см

Составляем два уравнения с одной неизвестной (Х).

Для этого складываем обе стороны и получаем: АВ + АС + ВМ + СМ + 2Х = 114

Отрезки ВМ и СМ равны, так как АМ — это медиана. При этом они в сумме составляют сторону большого треугольника ВС.

С учетом новых данных уравнение приобретает следующий вид: АС + АВ + ВС + 2Х = 114, где АС + АВ + ВС — это площадь большого треугольника. По условию задачи она равна 80 см.

Теперь уравнение имеет такой вид: 80 + 2Х = 114

Решение очень простое: 2Х = 114 - 80, 2Х = 35, Х = 17

Медиана в алгебре и геометрии

Термин медиана используется не только в геометрии, но и в алгебре. Если с геометрией все наглядно и понятно, то в алгебре это название обозначает середину числового ряда. В качестве примера можно привести простую последовательность: 1, 3, 5, 7, 9. В этом случае число 5 будет медианой.

Алгебраическое понятие широко используется в статистике, позволяя более точно определить середину числового ряда. Среди практического применения — методы анализа различных показатели (уровень доходов определенной группы лиц, какой размер одежды или обуви чаще всего продается в магазине за конкретный период).

Медиана в алгебре и геометрии — это совершенно разные понятия. Несмотря на это, они имеют одно общее свойство — обозначают середину конкретного объекта или числового ряда.